Study on the Hydration Kinetics of Raw Magnesium Oxide for Silicon-Steel Grade Magnesium Oxide

---

1. Introduction

Whether magnesium oxide is used to produce magnesium oxysulfate cement, magnesium hydroxide, or used as a refractory material, there are specific requirements for its hydration performance. MgO used for producing magnesium oxysulfate cement and magnesium hydroxide requires good hydration properties to facilitate the conversion into the target products. Conversely, MgO used for refractory materials requires low hydration properties. Therefore, it is necessary to study the hydration performance of magnesium oxide to meet various industrial needs [1-5]. This paper primarily investigates the hydration kinetics of raw magnesium oxide used for the preparation of silicon-steel grade magnesium oxide. Under the condition of sodium acetate presence, the hydration of magnesium oxide exhibits characteristics such as high hydration rate and ease of filtration and washing.

2. Experimental Part

2.1 Experimental Materials

The magnesium oxide used in the experiment was obtained by dissolving and purifying bischofite (MgCl₂​⋅6H₂​O) from the Qarhan Salt Lake, followed by spray thermal decomposition at 500°C in a vertical spray thermal decomposition furnace. The raw MgO passed through a 100-mesh standard sieve. Its main components are shown in Table 1.

Table 1: The composition of magnesium oxide (%)

Component	MgO	MgCl2	NaCl	KCl
Content (%)	94.2	2.2	2.1	0.8

Chemical analysis shows an MgO content of 94.2%, with a small amount of undecomposed MgCl₂ (2.2%) and other components being small amounts of soluble potassium and sodium chlorides. The particle size distribution of the MgO used is shown in Fig. 1, with D₁₀​=1.943μm, D_50​=8.272μm, and D₉₀​=23.099μm

.

2.2 Hydration Experiment

1. Hydration Principle: The hydration equation of magnesium oxide is: MgO+H₂O=Mg(OH)₂↓
2. Experimental Steps: Weigh a certain amount of MgO and add the hydration agent sodium acetate (dosage: 3.15% of the MgO mass). Measure distilled water (6 times the mass of MgO) and add it to a three-necked flask placed in a water bath for heating. When the required temperature is reached (actual temperature = set temperature ±3°C), add the weighed MgO and the hydration agent anhydrous acetic acid (dosage: 4% of the MgO mass). Start stirring for a set hydration time. Afterward, filter the slurry and wash the filter cake repeatedly with distilled water and anhydrous ethanol. Place the washed filter cake in a drying oven at 120°C for 24 hours before analyzing the hydration rate [6-8].

Table 2: The conditions of hydration experiment

Temperature (°C)	Time (h)
45	0.5, 1.0, 1.5, 2, 2.5, 3
60	0.5, 1.0, 1.5, 2, 2.5, 3

2.3 Calculation Formula for MgO Hydration Rate

The conversion rate of magnesium oxide is calculated according to the following three formulas:

1. C_Mg(OH)2 + CMgO = C _{Mg2 +} ，
2. C_Mg(OH)2VM_Mg(OH)2+C_MgOVM_MgO=mP
3. X=100C_Mg(OH)2\C_MgO + C_Mg(OH)2

Where:

• XXX : Hydration rate of magnesium oxide (%)
• CCC : Molar concentration ( mol⋅L−1mol \cdot L^{-1}mol⋅L−1 )
• VVV : Volume of solution (L)
• MMM : Molar mass ( g⋅mol−1g \cdot mol^{-1}g⋅mol−1 )
• mmm : Mass of magnesium oxide (g)
• PPP : Purity of magnesium oxide
• The concentration of magnesium ions in the solution is analyzed using EDTA titration.

2.4 Experimental Results

Table 3: The magnesium oxide hydration ratio at different times and temperatures (%)

Time (h)	Hydration ratio at 45°C (%)	Hydration ratio at 60°C (%)
0.5	30.08	47.48
1.0	45.32	74.65
1.5	53.92	88.76
2.0	64.31	95.23
2.5	71.06	100.00
3.0	78.21	100.00

2.5 Data Processing

The data from the hydration experiment was processed to obtain the fitting curve of MgO concentration vs. time (Figures 2 and 3). Based on these curves, the reaction rates at various points were determined (Table 4).

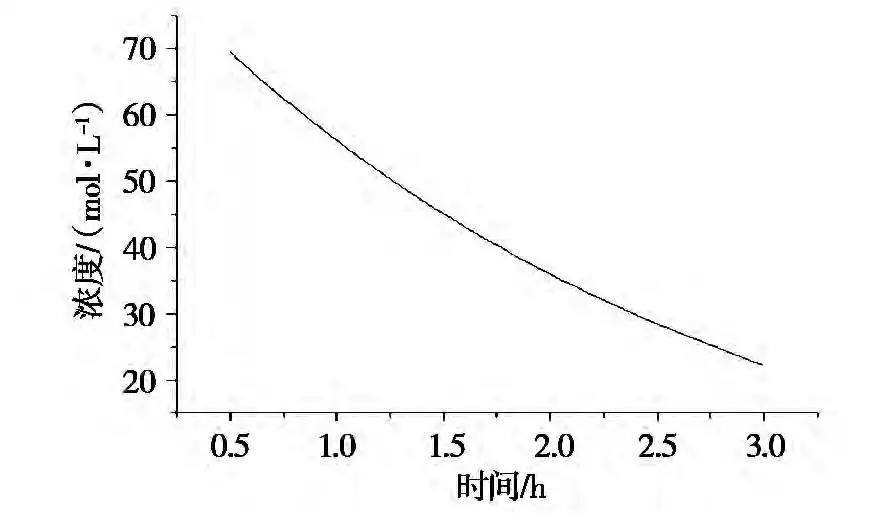
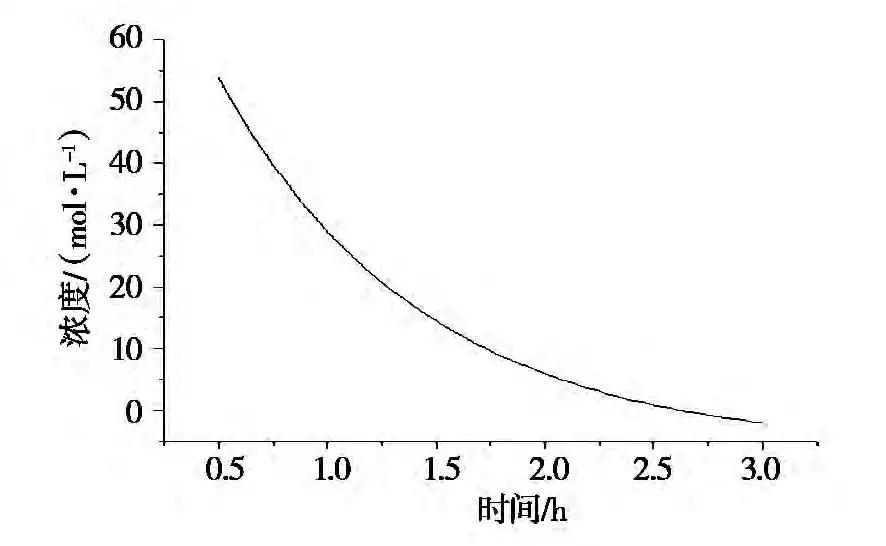
Table 4: The relation of time and rate at different temperatures

Temperature / °C	Time / h	Concentration / ( mol⋅L−1)	Rate / ( mol⋅h−1 )
45	0	1	0.601 6
	0.5	0.699 2	0.435 2
	1	0.564 8	0.238 4
	1.5	0.460 8	0.207 9
	2	0.356 9	0.171 4
	3	0.289 4	0.139
	0	0.217 9	0.143
60	0.5	1	0.949 6
	1	0.525 2	0.746 5
	1.5	0.253 5	0.412 8
	2	0.112 4	0.205 8
	2.5	0.047 7	0.112 4
	3	0	0.095 4

3) Determination of the rate equation via DPS data analysis. Based on the reaction rate equation r=kcⁿ, DPS data processing software was used to perform power function regression on the obtained data to calculate the reaction rate constant k and the reaction order n. The results are shown in Figure 4 and Figure 5.

From Figure 4, the kinetic regression equation at 45°C is derived as: Y₁=0.601526×X₁^1.2236

From Figure 5, the kinetic regression equation at 60°C is derived as: Y₂=0.992090×X₁^0.635462​

Table 5: Regression analysis of variance at 45°C

Source of Variation	Sum of Squares	Degrees of Freedom	Mean Square	F-value	p-value	Multiple Correlation Coefficient	Coefficient of Determination
Regression	0.611 7	1	0.611 7
Residual	0.021 3	4	0.005 3	115.005 0	0.000 4	R=0.9831	RR=0.9664
Total Variation	0.633 0	5	0.126 6

---

Table 6: Regression analysis of variance at 60°C

Source of Variation	Sum of Squares	Degrees of Freedom	Mean Square	F-value	p-value	Multiple Correlation Coefficient	Coefficient of Determination
Regression	0.175 8	1	0.175 8
Residual	0.009 0	5	0.001 8	97.219 6	0.000 2	R=0.9752	RR=0.9511
Total Variation	0.184 8	6	0.030 8

Interpretation of Main Results: For the power function regression model, a larger F-value is preferable; the higher the F-value, the more significant the regression model. If the F-value is too small, the regression equation is not significant, making it unsuitable for power function model analysis. The significance level (p) should be less than or equal to 0.05, indicating that the factor is statistically significant. The F-values, p-values, and correlation coefficients of both regression equations meet the necessary requirements, demonstrating that the regression equations fit the actual conditions well (Table 5, Table 6).

Based on the data processing and analysis described above, it was determined that the magnesium oxide (MgO) hydration reaction is a simple order reaction—specifically, a first-order reaction. The calculated chemical reaction rate constant (k) at 45°C is 0.601,526 h⁻¹, and the rate constant at 60°C is 0.992,090 h⁻¹ . Using the Arrhenius equation, the activation energy (E_a) for MgO hydration was calculated to be 29.6 kJ⋅mol⁻¹ , and lnA was found to be 7.6911 mol⁻¹⋅dm³⋅s⁻¹ . Based on the calculated activation energy data, the magnesium oxide used in this experiment exhibits high activity. The relatively small activation energy required for the reaction indicates that this hydration reaction proceeds with relative ease.

2.6 Results and Discussion

1. Optimal hydration conditions for the raw magnesium oxide used in preparing silicon-steel grade magnesium oxide:
   • Hydration temperature: 60°C
   • Hydration time: 105 min
   • Liquid-to-solid ratio: 4 (mass ratio)
   • Aging time: 4 h
   • Hydrating agent (Acetic acid): 4%
   • Hydrating agent (Sodium acetate): 3.15%
   • Washing water volume: 1 time the mass of the raw material (post-filtration)
   • Stirring speed: 120 r/min
2. Preliminary studies on the kinetics of magnesium oxide hydration found that the process follows a single first-order reaction. Kinetic equations for MgO hydration at different temperatures were established, and the activation energy ( EaE_aEa​ ) was determined to be 29.6 kJ⋅mol−1 with lnA at 7.6911 mol⁻¹⋅dm³⋅s⁻¹.
3. The XRD pattern of the magnesium hydroxide ( Mg(OH)₂​ ) obtained under optimal hydration conditions is shown in Figure 6. The XRD results show that after the raw magnesium oxide is hydrated under optimal conditions, the product has high purity with virtually no impurity peaks, confirming that the product is a pure phase of magnesium hydroxide.

4. Figure 7 shows the TG-DTG curves for the hydration product, magnesium hydroxide, obtained via thermogravimetric analysis.

Table 7: Chemical analysis of magnesium hydroxide products (%)

Component	Mg(OH)2​	NaCl	KCl
Content (%)	99.25	0.013	0.031

---

According to the TG-DTG curves, the product exhibits only a single decomposition peak corresponding to magnesium hydroxide, indicating that the magnesium hydroxide product exists as a pure phase. This validates the results obtained from the XRD analysis. Further chemical analysis of the product (Table 7) reveals that the purity of the magnesium hydroxide reaches 99.55%, fully satisfying the requirements for the preparation of silicon-steel grade magnesium oxide.